Null hypothesis and p-value
It’s difficult for us today to imagine a situation in which some newfound scientific knowledge is accepted by the society and the scientific community without a solid evidential background.
But it wasn’t always like this – the strict requirement to substantiate hypotheses and theories with empirical data is a recent innovation. Even in the mid-20th century, plenty of influential theories in social science, economics, and psychology were just that – pure theories, Sigmund Freud’s psychoanalytic theory being the most well-known example. It had a massive effect on culture, society, and science even though it was developed without any experiments, verification, or clear empirical data.
Examining the structure of any contemporary research article, we’ll always find at least some empirical research accompanied by mathematical analysis.
Let’s say some scientists, like biologists or medical researchers, want to test a hypothesis: they have ten patients who they’d like to study and, based on that small sample group, to put forth a scientific assertion about the general population. First, they must propose a null hypothesis – one that’s formulated as the lack of differences, lack of influence, lack of effect.

Maybe these scientists have invented a new vaccine and wish to test its effectiveness. The null hypothesis would be that the new vaccine is going to be as effective as a placebo, or a dud. Next, the scientists conduct tests, observe, and compare the collected data with their null hypothesis. Now, they see that the sample group of those who received the vaccine has 20% more recovered patients than the placebo group. Knowing that the sample sizes were very small, we could suggest that this is a coincidence, a random outcome, or the effect of hidden, unaccounted-for factors.
That’s why mathematicians have come up with a trick: even though there’s only one sample group, and a small one at that, we can still infer what the results would be if we conducted not one, but infinite experiments with many groups. Here’s a simple analogy: on a regular dartboard, there are always more hit marks near the center and less around the edges. Even though none of our darts may hit the bullseye, the average result would still place us very close to it.

Conducting just one experiment or throwing a single dart won’t tell us anything. But may hypothesize as to what the hit spread would look like within the current reality. Next, some simple math allows us to show how well the observed results match the initial hypothesis.
In the vaccine case, researchers can well use the acquired empirical data to reject their null hypothesis and claim that the vaccine works, as the likelihood of an accidental 20% recovery increase is extremely small. This method is referred to as the p-value, or the likelihood of obtaining similarly extreme results in repeat attempts on the condition that the null hypothesis is correct.
Statistics and the issues of modern science
An overwhelming majority of today’s scientific articles, and the general idea of what makes scientific knowledge, are based on a key criterion: statistical validity. This is especially sensible in the case of various empirical research.
Statistics helps us tell science and pseudoscience apart, understand which data is right and whether we should believe it. On the other hand, these very same statistical methods, when incorrectly interpreted, are also used by pseudoscientists – and that’s a big problem.
Today’s statistical science was essentially founded by two men: biologists and mathematicians Karl Pearson and Ronald Fisher. They came up with pretty much all of the methodology we use today: the theories of correlation and distribution, decision-making algorithms, and much more.
All of statistics answers one general question: if our null hypothesis is correct, then what is the likelihood of acquiring the same results, or even more extreme ones? In other words, how well the observed empirical reality aligns with the null hypothesis. This is a base definition of how statistics approaches matters of the world.

Today’s academic community follows a certain golden rule: that a p-value must always be below 0.05. If it is less than 0.05, it is reason enough to reject the null hypothesis and accept the alternative one.
P-value has become a social element of science. Many important decisions depend on it: whether to share research findings with the public, to publish them in a scientific journal, to allocate funding for further research, and so on.
For instance, major peer-reviewed journals prefer research that has produced results with a p-value below 0.05. But a number of issues arose in the scientific world, because the system adapted to the rules of the game. Forcing researchers to produce statistically significant results made them abandon all research that couldn’t make the threshold. Even though the knowledge that a hypothesis hasn’t been confirmed is as important to science as when it has.

Another serious issue even has its own name: p-hacking. Even top journals like Nature regularly find themselves in the middle of a controversy when it is revealed that researchers have manipulated their numbers to achieve the coveted p-value.
The funny thing is that the threshold was created almost randomly. The 0.05 value was taken from one of Pearson’s early works in which he wrote something along these lines: “p-value doesn’t tell us if we’re right or wrong. It is a mathematical value that provides a purely mathematical proof of correctness of a hypothesis. The number 0.05 can be seen as a symbolic threshold, but there is no sense in relying on it exclusively.” As it so often happens, people only remembered the number. For many years, it became a key element of statistics. It’s even integrated into statistical software which will notify you if the results are below 0.05 and are, therefore, unscientific.

Should we give up on statistical methods?
So how do we know if statistics was applied correctly and the results are reliable? Inevitably, we fall into a trap: as soon as you introduce rules, the system adjusts to them. There are always those who will, instead of only sharing results where everything was done right and the required p-value was achieved, try to outsmart the system. Such scandals break out at the highest levels of modern science.
There’s no obvious solution to this problem. Some propose altogether canceling the idea of a certain threshold and letting scientists publish all their work as is – a sort of open science paradise. This is at the leftmost edge of the scale, a response in opposition to the despotic rules employed by scientific journals.

But it’s tough to implement. Clearly, some entry threshold must still exist. That’s why people try to come up with a new approach. For instance, an increasingly popular idea is that scientific articles should be published along with all the data and computation logs, including the scripts – in R, Python, or other programming languages – that would allow anyone to reproduce the results. Understandably, someone who just wrote in the right numbers would have trouble passing this threshold. But the issue is that as soon as you build new safeguards, people find new loopholes.
That’s why scientists are moving even further and proposing to do all of the aforementioned as well as disclose which hypotheses you’re testing in advance. So, long before publishing an article, researchers would say: we’re currently conducting experiments at the lab in which we want to test these hypotheses. The issue is that this is almost always a half-truth: usually, they already have some material to work with, some minimal results, which they present as mere ideas. The nature of this is, once again, purely social.
It’s well understood that research is funded via grants. How does that work? Researchers apply for grants and describe their hypotheses and the results they expect. Once they’re done, they report on how they succeeded or failed to verify the hypothesis.
It so happens that most of these reports are purely positive: we’ve achieved exactly what we planned to. And the reason is the same as with publications: negative data just isn’t in demand. Sometimes, a researcher or a team is given a sizable grant, they spend a year working on it, and end up with nothing but a rebuttal of their hypothesis.

From a scientific standpoint, that’s a completely normal situation that occurs in 99% of cases. Breakthroughs are the result of years of work and thousands of failed attempts. But as soon as we encounter any social institution, it suddenly becomes a challenge to admit you’ve failed.
This is a very complex issue that’s difficult to get out of but, nevertheless, we’ve at least come to the point where we are discussing it. Modern science in general is experiencing a lot of turmoil. Take the recent crisis of the reproducibility of classic psychological and social experiments of the 70s and 80s. This obsession with only publishing good, positive results is what has led us to that crisis.
Right now, the emphasis is shifting from re-calculating all sorts of statistical data to actually reproducing the results and having the experiments repeated by other researchers in other conditions. That is the only way to make sure that the findings are truly objective. Now considered proper research etiquette, it will likely become a mandatory requirement in the near future. Because the idea that objectivity can only be measured with p-value is, of course, an illusion. Some journals have gone as far as forbidding the publication of p-value results, instead preferring Bayesian statistics, which have lately become more popular.
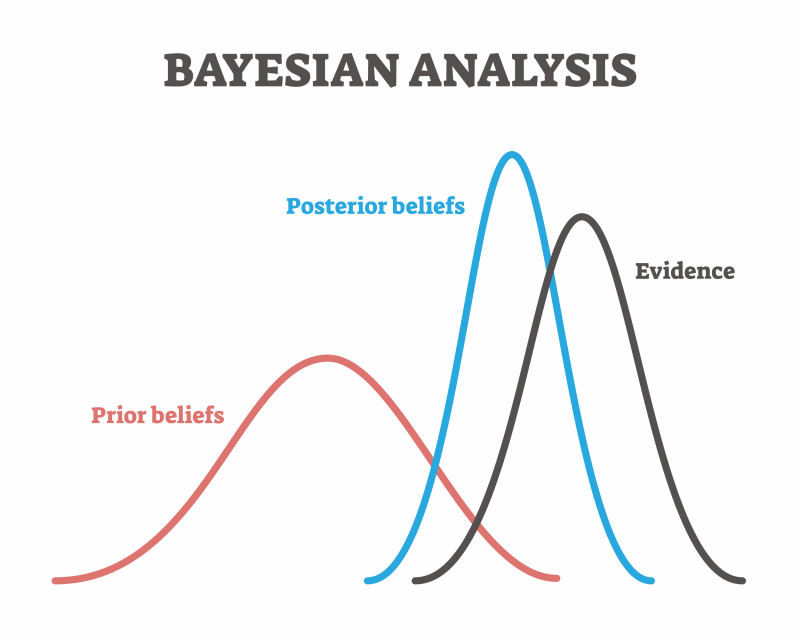
Bayesian statistics is a method of calculating the validity of hypotheses and assertions using existing evidence such as data and empirical observations. Simply put, a hypothesis is more valid the better it explains the existing facts. The more ways there are to explain the facts, the less valid a hypothesis is.
As p-value is a rather abstract measurement that doesn’t check the probability of hypotheses, Bayesian statistics, according to some, is a more accurate method.
Science and pseudoscience
How is the objectivity and reliability of scientific knowledge verified today? The first, most high-level approach, asks us: does this knowledge fit into the existing scientific model of the world? Secondly, was the research conducted properly? Thirdly, was the data processed properly? Finally, was the data processed properly by third parties and reproduced? The latter question is now seen as especially important.
The Russian Academy of Sciences has a whole department dedicated to dealing with pseudoscientific research. It is a large and important issue, as pseudoscience isn’t just wrong, but also potentially harmful to people and the world.

So how do we understand what is science and what is pseudoscience? Karl Popper had some ideas on how to classify scientific knowledge; he believed that the only scientific knowledge is that which can be shown as false. That is Popper's falsification principle, and it is the opposite of verifiability: the latter asks us to find evidence of a hypothesis, while the former asks us to find evidence to the contrary.
That, and not statistical confirmation is the main principle of authenticity of scientific knowledge. Psychoanalytic theory was strongly criticized precisely because, in its classic form, it is highly difficult to disprove.