A Brief Guide to Artificial Intelligence
An artificial neural network is a mathematical model inspired by the anatomy of the brain. It has been shown to be very powerful at helping computers solve problems that previously only humans could do. A neural network consists of "neurons" - computing units often expressed by simple mathematical functions. The neurons feed their outputs as each other’s inputs and are typically organized in connected layers. When designing a neural network it is important to consider the shape or topology of how said neurons are connected. Modern networks can have up to 10 layers and even more (for comparison, the human neocortex has 6 layers).

An artificial neural network is a mathematical model inspired by the anatomy of the brain. It has been shown to be very powerful at helping computers solve problems that previously only humans could do. A neural network consists of "neurons" - computing units often expressed by simple mathematical functions. The neurons feed their outputs as each other’s inputs and are typically organized in connected layers. When designing a neural network it is important to consider the shape or topology of how said neurons are connected. Modern networks can have up to 10 layers and even more (for comparison, the human neocortex has 6 layers).
The easiest algorithm for optimization is called gradient descent. It is also the basis for many other algorithms. It’s an iterative process and the main idea behind the algorithm is very simple: at each step go down the steepest direction of your error function J.
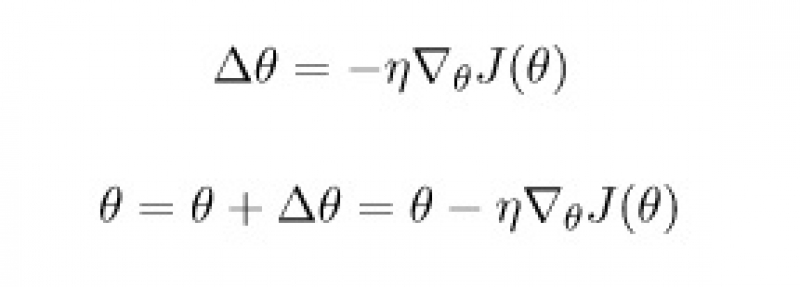
A derivative of a function will tell you the said direction, but the tricky part is choosing the size of your step Θ. When it is too big the algorithm "overshoots" the minimum, and when Θ is too small the gradient descent takes a long time to converge (find the minimal point). Choosing a small step can also lead to getting stuck in a small local pit, instead of finding the global minimum.
Nesterov Accelerated Gradient is an improvement over the standard gradient descent. The idea is to not only use the information at the current point but to also remember the path that we were taking. If we were moving in the right direction then we should continue in that direction. In mathematical terms, it means we should calculate the "moving average", and use it as the size of our step.
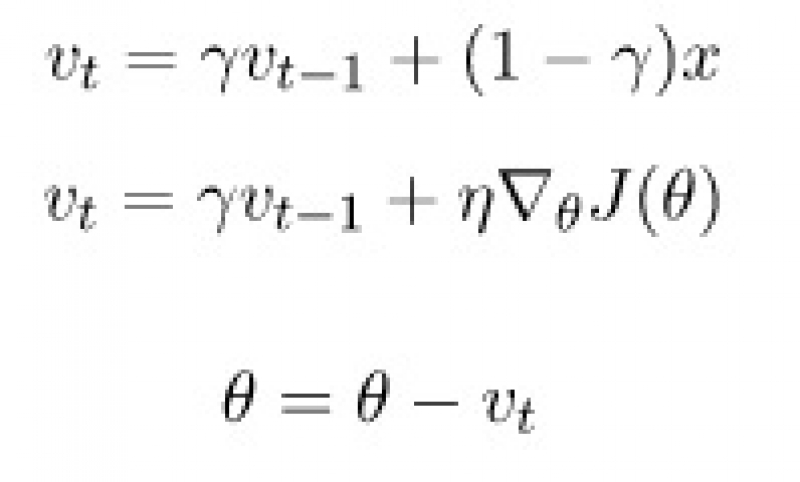
The coefficient y can be anywhere between 0 and 1. It determines how much influence the history of x has on the algorithm. When y is close to 0 NAG behaves like regular gradient descent. Nesterov algorithm has many variations: it can not only use information from the past but also make glimpses into the future by calculating some of the future points and averaging them out. There are also different methods for calculating the average, besides the moving average.
Adagrad (adaptive gradient) is a method that helps to weed out insignificant features in the data. To do that, we will calculate the sum of squares of its updates for each parameter. If a certain parameter is activated by neurons very often, then the sum will become large quickly
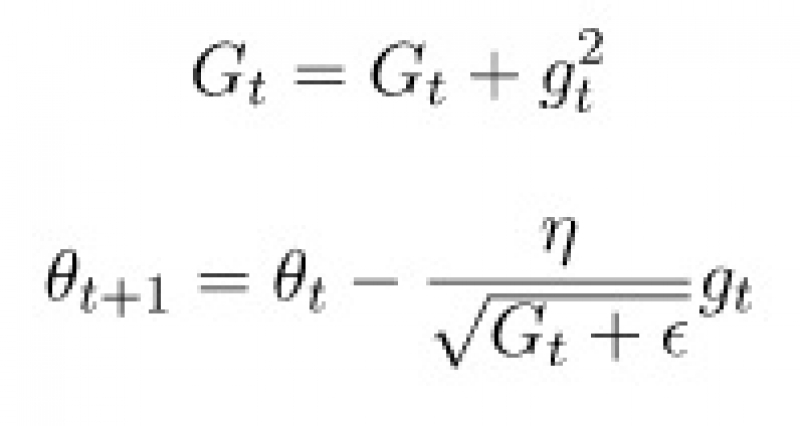
Gt is a sum of squared updates and is just a small number that’s needed to avoid division by zero. So, the idea of Adagrad is to use something that reduces updates for elements that we already update frequently. No one forces us to use this particular formula, so Adagrad is sometimes called a family of algorithms. For example, we can remove the root or accumulate modules instead of squared updates. One of the advantages of Adagrad is that there is no need to accurately select the learning rate. It is easy to set the rate moderately high, but not so huge that the algorithm diverges.
In conclusion, I have reviewed some of the most popular neural network optimizers. I hope that artificial intelligence will no longer seem like a mysterious black box full of magic, but rather an elegant mathematical and computational tool.
