Доктор физико-математических наук и профессор факультета фотоники и оптоинформатики Университета ИТМО Юрий Рождественский, а также молодые ученые Семен Рудый и Татьяна Вовк опубликовали научную статью по распознаванию подписей человека с помощью методов фрактальной размерности Минковского и машинного обучения.
«Мы рассматриваем подпись человека как траекторию кончика пера, которая описывается уравнениями Ланжевена (стохастические дифференциальные уравнения, описывающие броуновское движение). Для подписи, рассматриваемой таким образом, можно вычислить фрактальную размерность Минковского. Данный параметр отличается для оригинальных и намеренно фальсифицированных подписей, что позволяет надежно различать похожие друг на друга подписи, оставленные разными людьми», – объяснила Татьяна Вовк.
Предлагаемый подход в сочетании со стандартными методами машинного обучения – потенциально мощный инструмент для идентификации и проверки подписей и любых других видов обозначений. В данном случае, по словам Юрия Рождественского, машинное обучение служит для нахождения похожих подписей и отделения разных по форме подписей друг от друга. В свою очередь, метод фрактальной размерности позволяет с высокой степенью точности определить, подделана ли подпись, в то время как машинное обучение не справляется с этой задачей.
Фрактальная размерность Минковского
Фрактальная размерность Минковского, или дробная размерность, пришла из хаотической динамики (раздел физики). Про дробную размерность обычно рассказывают на примерах различных ломаных, таких как кривая Коха. В начале берется отрезок, делится на три равные части и средняя часть заменяется на два отрезка, равных изъятому. Получается ломаная из четырех равных отрезков. На следующем этапе действия повторятся с каждым из четырех отрезков, и получится ломаная из 16 отрезков. Эти построения повторяются бесконечное число раз и в итоге получится ломаная, состоящая из бесконечного числа отрезков. Сколько бы ее не масштабировали, все равно будет получаться одно и тоже.
Такой тип структур называют фракталами. Они встречаются повсеместно, например, в структуре деревьев и их листьев, корней, в кристаллах. Кроме того, геометрическую фигуру треугольник можно до бесконечности делить на меньшие треугольники, таким образом тоже получая фрактальную структуру.
«Существует проблема береговой линии, когда невозможно точно измерить ее длину – чем меньше будем брать масштаб (или цену деления линейки, с которой мы ходим вдоль берега и измеряем ее длину), тем больше будет получаться ее длина. Представьте, что вы хотите измерить береговую линию острова. Измеряя ее разными способами – веревкой, метровой, сантиметровой или миллиметровой линейкой, мы будем получать разные значения. Фрактальная размерность Минковского – это характеристика этой длины, предел всех дроблений», – объяснил Семен Рудый.

В данном случае, чтобы определить, поддельная ли подпись, необходимо взять оригинал подписи и измерить ее фрактальную размерность, чтобы затем сравнить с исследуемой подписью. Если подпись поддельная, то фрактальные размерности оригинала и подделки будут отличаться.
«Вы можете нарисовать гладкую кривую, например, круг на компьютере и посчитать ее фрактальную размерность, которая всегда будет одна и та же независимо от размера и толщины линии. Однако, если два человека нарисуют по кругу, то фрактальная размерность этих кругов будет отличаться. Почему? Все просто – потому что мы разные. Когда машина определяет подпись человека, для нее не имеет значения, что это за человек, о чем он думал, как держал руку. Фрактальная размерность об этом тоже “не думает”, однако она была создана физиками для описания физических стохастических систем (стохастический процесс – это процесс, поведение которого не является детерминированным, и последующее состояние такой системы описывается как величинами, которые могут быть предсказаны, так и случайными. – прим.ред.). Именно по этой причине фрактальная размерность наиболее адекватна к нашей физической реальности. Подпись человека – совокупность случайных и детерминированных факторов, наша задача выделить детерминированные, в то время как случайные для нас неважны», – объяснил Юрий Рождественский.
Как посчитать фрактальную размерность
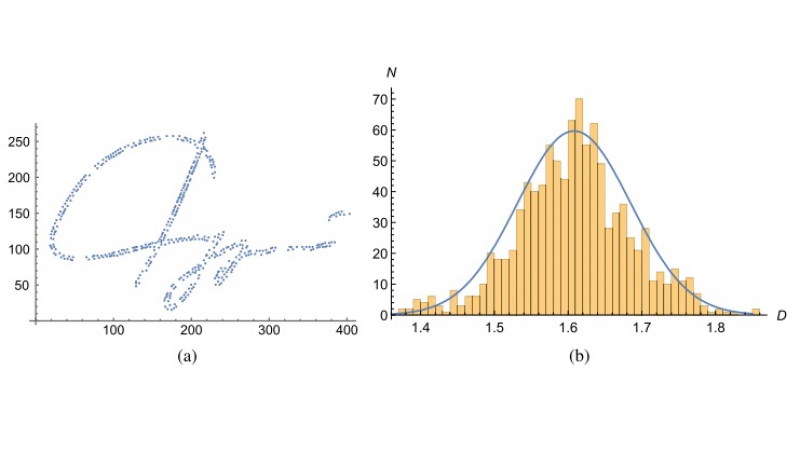
Исследователи рассматривают любую подпись как траекторию некоторой частицы, двигающейся согласно уравнениям хаотической динамики. Анализ данной траектории выполняется путем дискретизации подписи с помощью сечения Пуанкаре. Данная процедура заключается в том, что от подписи берется по точке через определенный период времени. Совокупность полученных точек на плоскости и есть двумерное отображение Пуанкаре. Далее уже дискретизированный вариант подписи анализируется с помощью фрактальной размерности. Плоскость с набором точек разбивается на четыре равных квадрата. Квадраты, внутри которых есть точки от подписи, разбиваются еще раз, также на четыре равных квадрата поменьше. Так продолжается до тех пор, пока количество квадратов с точками не начинает сохраняться. Именно этот параметр определяет дробную размерность.

«К подписи применяется сечение Пуанкаре, это несложная процедура. У каждой траектории можно выделить следующие оси: ось координат, ось скоростей и ось времени. При сечении Пуанкаре подпись-траектория по оси скоростей разбивается на равные промежутки времени. Получающееся множество точек, в свою очередь, накладывают на плоскость координат и скоростей, составленную из соответствующих осей, и множество точек увеличивается. Полученный итоговый набор точек анализируется с помощью наложения сетки одинаковых квадратиков. После наложения мы считаем квадратики и смотрим, сколько квадратиков заняты хотя бы одной точкой, и записываем данные – отношение занятых квадратиков к полному их количеству. Затем мы увеличиваем количество квадратиков в сетке в четыре раза, и мы снова производим ту же процедуру и записываем отношение. Так мы будем делать до тех пор, пока в каждой занятой клетке не будет по одной точке. Дальше уменьшать не имеет смысла, так как число занятых квадратиков останется прежним. Предел отношения количества квадратиков и называется фрактальной размерностью. Для нашей задачи мы производили порядка 20-30 уменьшений. Если этот процесс автоматизировать, то он сможет занимать минуты. Это еще один плюс разработки, ведь вопрос подлинности электронной подписи – это всегда вопрос времени», – объяснил Юрий Рождественский.
Как сегодня проверяют подлинность подписи
Подпись – уникальный и важный биометрический маркер человека. С древних времен этот маркер использовался в качестве персонального идентификатора. Даже сегодня, несмотря на разработку методов автоматического распознавания и проверки подписей, в большинстве случаев подлинность подписи проверяется экспертами вручную. Как правило, распознавание подделок определяется с помощью почерковедческой экспертизы, которая проводится криминалистами.
«Фактически криминалисты сравнивают на глаз два текста по написанию букв. При этом человек в разные годы и даже в разное время суток может подписаться совершенно по-разному. Хотелось бы иметь объективный инструмент, который давал бы конкретные критерии определения подделки. Такая же проблема с определением подписи на предметах искусства. Такую экспертизу может проводить только эксперт. Зная, какие суммы в этой сфере фигурируют, мы не можем быть на 100 % уверены в качестве экспертизы, даже учитывая репутацию и авторитет эксперта, человеческий фактор никто не отменял», – прокомментировал Юрий Рождественский.
Где метод можно применять
Потенциальное применение такого метода не только при идентификации подписей частных лиц, но и при исследовании объектов искусства на предмет подделки. Если в первом случае исследователи работают с единичной подписью, то в случае предметов искусства исследователям необходимо анализировать кривые на изображении – по анализу этих кривых и определяется, поддельная картина или нет.
«Подпись – это кривая. Мы берем картину, на ней много кривых. В данном случае мы можем использовать такой же метод – взять контуры линий на картине, провести анализ и выявить их фрактальную размерность. Затем мы берем другую картину, авторство которой хотим узнать. Речь о том, что рука и взгляд художника поставлены определенным образом, он по-своему видит действительность, и когда он пишет картину, он не проводит линии произвольно, у него есть внутренняя логика. Согласно нашей гипотезе, независимо от сюжета картины, эта внутренняя логика должна проявляться, и именно она позволит определить авторство», – объяснил Юрий Рождественский.




