Многие устройства — колеса автомобилей, электродвигатели, турбины самолетов и атомных электростанций и самые обычные бытовые приборы — не монолитны и состоят из разных деталей. Они соединяются механически и в процессе работы между ними неизбежно возникает трение. Это приводит к быстрому износу, поэтому специалисты ищут разные способы улучшить сцепление и сделать контакт более гладким.
Чтобы лучше понимать, как происходит сцепление между поверхностями в зависимости от их гладкости или шершавости, физики и материаловеды изучают параметры внешнего облика и текстуры рельефов. Традиционно рельеф измеряют с помощью физических методов: атомно-силовой микроскопии, профилометрии или спутниковых измерений — в зависимости от масштаба объектов. Однако эти методы не способны определять некоторые важные особенности рельефа, от которых зависят свойства поверхностей и материалов. Например, латеральные характеристики (описывают направление неровностей) и многомасштабные (описывают шероховатость на разных уровнях увеличения масштаба). Для решения этой проблемы используют математические инструменты, которые позволяют определять эти характеристики на основе данных. При этом большинство существующих подходов также работает с ограниченными масштабами поверхностей: либо с нано- и микроскопическими размерами (например, наночастицами), либо с макроуровнем (например, спутниковыми снимками поверхности Земли).
Схемы модели, мысленного эксперимента, предлагаемого метода и алгоритма: A) Механизм контакта двух текстурированных поверхностей, иллюстрирующий условия трения покоя или скольжения; Б) Концептуальный мысленный эксперимент, моделирующий контакт текстурированного, абсолютно пластичного тела с идеально гладким, абсолютно жестким телом; В, Г) Принцип работы алгоритма, продемонстрированный с использованием карты высот рельефа поверхности. Изображения предоставлены спикером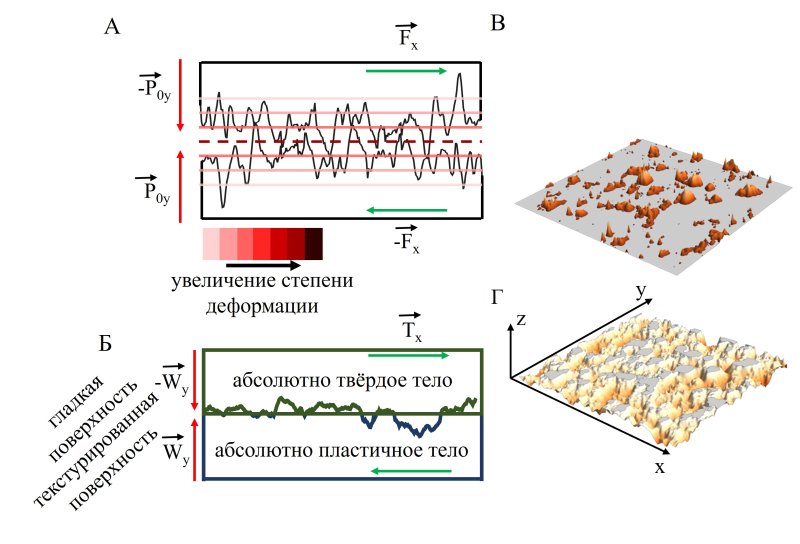
Физики из ИТМО создали новый алгоритм для анализа параметров рельефа поверхности почти любого размера — от наноразмерной текстуры тонких полимерных пленок до макроразмерных данных о топографии горных хребтов Земли. На основе данных о поверхностях модель показывает, как они будут взаимодействовать между собой, и позволяет ответить на важный для физики вопрос: в какой момент два «шершавых» тела, приложенных друг к другу, начнут проскальзывать. Для этого она анализирует карты высот рельефа поверхности любых размеров — от единиц нанометров до нескольких километров и рассчитывает количество, геометрические и топологические характеристики формы контактных площадок.
Данные о высоте рельефа загружаются в модель в виде квадратной матрицы, каждый пиксель которой обозначает высоту в конкретной точке. Затем программа рассчитывает перепад между максимальной и минимальной точками рельефа, и этот диапазон делится на определенное количество уровней давления. На последнем этапе модель определяет, как рельеф поверхности будет контактировать с другой поверхностью на каждом из этих уровней.
Рельеф поверхности A) полиионной сборки; Б) микрокристаллов ZnO; В) Гранд-Каньона; Г, Д) синтетических рельефов. Изображение предоставлено спикером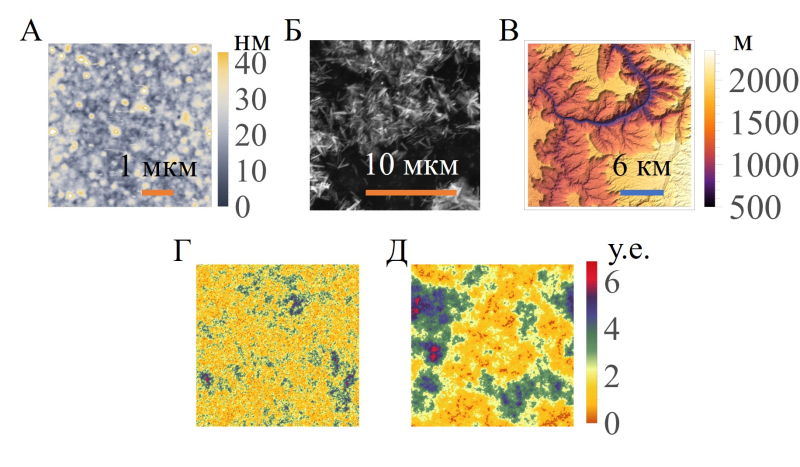
Для отработки метода исследователи использовали результаты атомно-силовой микроскопии (например, данные о рельефе поверхности пластины полупроводникового кремния, полимерных пленок, пленок из бактериального сырья, тонких пленок диоксида вольфрама), растровой электронной микроскопии (микрокристаллиты оксидов переходных металлов), «синтетические» рельефы, а также топографические данные различной местности: Карельских озер, Гранд-Каньона, гор Арарат и Фудзияма.
«Мы не только предложили новый метод вычисления важных признаков рельефа поверхности, но и открыли новое явление: вне зависимости от масштаба и природы поверхности, инструментов измерения, соотношения численных, геометрических и топологических параметров контактных площадок рельефа все поверхности развиваются очень похожим образом. Это означает, что все поверхности — и гора Фудзи, и наноструктурированная поверхность латуни подчиняются одним законам и реагируют на сжатие одинаковым образом. Новая гипотеза позволит быстро и точно прогнозировать взаимодействие поверхностей в разных областях — от микроэлектроники до геологии», — рассказал один из авторов исследования, инженер научно-образовательного центра инфохимии Александр Агликов.
Александр Агликов. Фото: Дмитрий Григорьев / ITMO NEWS
В перспективе новая модель поможет лучше понять процессы трения, износа и деформации объектов. Это пригодится при создании более износостойких покрытий и надежных механизмов, а также в исследовании поверхности Земли: например, чтобы определить, как образуется русло реки, из каких притоков она состоит, из какой площади собирает воду. Потенциально разработка может найти применение и в космических исследованиях: например, с ее помощью можно будет сравнивать ударные кратеры на различных космических телах и определять, насколько похожими были столкновения с метеоритами.




