Non-existence theorem
One of the most basic laws of physics is that energy, confined in some open system, will dissipate into the surrounding space. If you strike a drum, you’ll see the mechanical oscillations of its membrane, which are the source of the sound. In other words, the energy of the oscillations is transferred to the acoustic waves.
Any oscillations in open systems (i.e. systems that exchange energy with their surroundings) – such as tuning forks, strings, or optical resonators – will inevitably fade out. But in 1929, physicists Eugene Wigner and John von Neumann predicted the existence of specially constructed systems in which supporting states would not radiate energy into free space. Simply put, the energy would remain localized within the system. This phenomenon became known as bound states in the continuum (BICs). But according to one non-existence theorem, BICs cannot exist in finite systems.
Physicists from ITMO have discovered an exception to this rule: while the theorem does apply to optical and quantum processes, it’s not completely applicable in acoustics. Therefore, it should be possible to create a system in which the resonating object wouldn’t produce sound, ensuring that mechanical oscillations will remain in the system for an infinite period of time.
According to Ilya Deriy, a PhD student at the Faculty of Physics and the paper’s lead author, the reason for this is that acoustic oscillations have a more complicated structure.
“Wave propagation in solid states can be longitudinal or transversal. While both types can occur in solid bodies, only longitudinal oscillations can take place in liquids. That’s the key moment: if we take a solid object and induce only transversal oscillations in it, they won’t be able to induce longitudinal oscillations in a liquid. Therefore, we’ll have an open system in which there will be no transfer of the energy into surrounding space. These oscillations will remain for a very long time until they fade out due to losses in the resonator material,” says Ilya Deriy.
Ilya Deriy. Photo by Dmitry Grigoryev / ITMO.NEWS
Symmetry is key
In order for such a system to work, several conditions must be met. The first concerns the shape of the resonator, which must have rotational symmetry. In their research, the scientists considered a sphere in which the upper and lower halves rotate out of phase, all while the shape itself remains the same. But even the smallest change, such as a slight flattening of the sphere, will result in sound oscillations. The same will happen to any body of revolution, such as a cylinder or a spheroid.
The second important aspect is the surrounding medium. The effect manifests well in low-viscosity environments such as water or gas. In a more viscous medium, the surface of the resonator would “cling” on to the fluid and affect the system Q-factor – that is, the period during which energy will remain in the resonator. Finally, the Q-factor is affected by the very material that the resonator is made of: the less defects it contains, the better.
But the last two requirements aren’t as critical. As the scientists note, the viscosity of the medium and the material itself can affect the Q-factor, but overall they do not disprove the researchers’ calculations:
“We proved that in the cases of some fluids and almost all gases you don’t have to account for the viscosity of the medium since the material losses in the resonator have a bigger influence. And, despite the material losses, the Q-factor will still remain quite high,” explains Ilya Deriy.
Quadrupolar bound state in the continuum in a spherical acoustic resonator. Image courtesy of the research team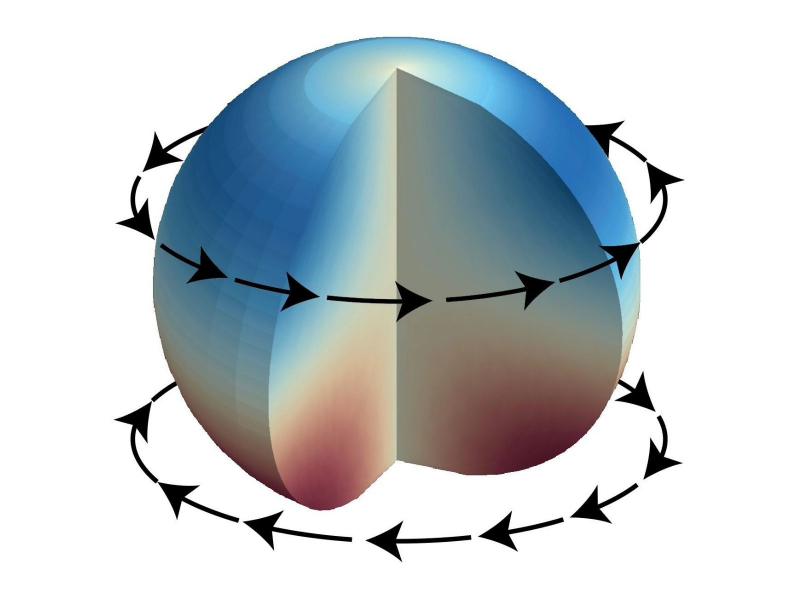
Bound states in the continuum
Presumably, such an effect – but with significant limitations – can be achieved in optical systems, too. For instance, in metals at plasma frequency. In this case, a metal’s dielectric permittivity will be equal to zero; in these conditions, it is possible to induce longitudinal electromagnetic waves – bulk plasmons. Since electromagnetic waves have a transversal polarization in free space, they will not exchange energy with bulk plasmons. But material losses in this case will be so significant that a high Q-factor could not be achieved.
BICs in optics, acoustics, and quantum mechanics have been discovered quite a long time ago. But according to the non-existence theorem, they would only exist in structures that are infinite in one- or two dimensions. In real, finite systems, they turn into quasi-BICs, which, if only a little, still exchange energy with the surrounding environment.
The main discovery made by the scientists is that finite systems can contain not only quasi-BICs, but genuine BICs, too:
“We demonstrated that you can find bound states in the continuum in finite acoustic structures thanks to an inconsistency between the polarizations of BICs and of waves in the surrounding environment. This is why we called them polarization-protected bound states in the continuum,” says Ilya Deriy.

Non-radiating oscillartions in a spherical acoustic resonator. Image courtesy of the research team
According to the researchers, polarization-protected BICs can advance the understanding of BICs in optics and quantum mechanics. But the scientists themselves plan to focus on acoustics specifically; their next step will be to study polarization-protected BICs experimentally. This research might lay a foundation for acoustic metasurfaces – which, in turn, can be used to develop highly effective sound dampeners, acoustic antennas, and sensors.
The research project was carried out with the support of the Russian Science Foundation.
Reference: Ilya Deriy, Ivan Toftul, Mihail Petrov, and Andrey Bogdanov, Bound States in the Continuum in Compact Acoustic Resonators. Physical Review Letters, 2022.