In 2012, Nobel laureate Frank Wilczek, who received the scientific world’s top honor "for the discovery of asymptotic freedom in the theory of the strong interaction,” posed a new fundamental question to the world’s scientists; this time, one based on Einstein’s theory of relativity.
Its basic summary may seem confusing to those not familiar with modern theoretical physics, quantum theory, and studies of the time-space continuum. Wilczek asked the following: if there are crystals that break the translational symmetry in space, could there be crystals that break it in time? Although previous research has indicated that these crystals cannot exist, physicists Valerii Kozin and Oleksandr Kyriienko have now described a model in which the existence of such crystals is possible. Since, by this point, anyone would have plenty of questions, we asked Valerii Kozin to provide a few explanations.

What are crystals and translational symmetry?
We’ve all gotten used to saying “crystal” to describe a grain of salt, a quartz shard in our wristwatches, or minerals found on museum displays and at jewelry stores. But to theoretical physicists, there is a deeper meaning to that word.
“Every day, we encounter many states of matter,” explains Kozin. “Those are solid, gaseous, and liquid substances. What do we know about solid bodies? If liquid and gaseous states of matter present a sort of “atomic soup,” solid bodies possess a crystal lattice, meaning that their atoms and molecules exist within a structure that follows a certain order of placement.”
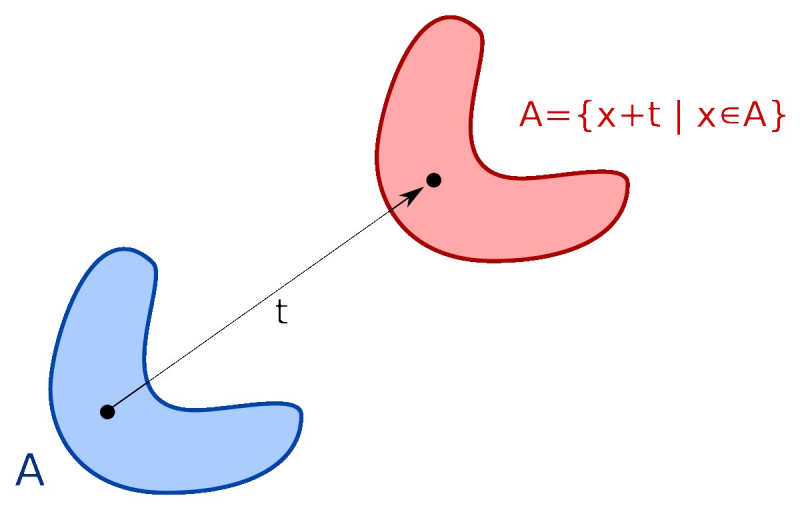
The elements of a homogenous structure that lacks the periodicity of a crystal lattice can be shifted by any distance; the system will remain unchanged. That’s translational symmetry. It doesn’t work with crystals. Imagine two square-ruled sheets of paper. If we lay one on top of the other and then shift it by the width of one square, nothing will change – the squares will still match. But if we shift it by more or less than a whole square, the system will begin to look differently. That’s what happens to the crystal lattice of solid bodies: its elements cannot be shifted farther or closer than the regular distance between two atoms. Otherwise, the structure will not connect with itself. That, in turn, is called a broken translational symmetry.
“Now, I must note something here,” says Kozin. “In this context, theoretical physicists are used to speaking about ideal, infinite crystal structures. In reality, we deal with finite pieces: a slab of iron, a shard of mica. Granite consists of a large number of small crystals, and if we were to examine it at the atomic scale, we’ll see that each crystal within a piece of granite is practically infinite since it contains around 10^23 atoms – a mind-boggling number, which is why we may disregard its finiteness for the purpose of theoretical calculations.”
Therefore, objects that possess a crystal lattice break the space-translational symmetry.
“Since, in theory, every crystal we encountered does this, scientists don’t use the term “space crystal.” But when we started to consider whether the same effect may exist in time, we began to speak of space crystals and time crystals,” explains Valerii Kozin.

The Einstein connection
Before the 20th century, scientists regarded time and space as two relatively independent concepts. This is well understood by anyone who’s ever taken public transport.
“Say you’re on a long-distance train that has great noise cancellation and rides along a perfectly smooth track. You wake up and feel no shaking, no rattle of the wheels, with the shades drawn. Would you be able to tell if the train is moving or not? The universal laws of nature would dictate the latter – if you bounce a ball off the floor, it’ll return to your hand in both cases. If you try to boil some cup noodles, it’ll cook whether or not you’re traveling; the lamp above your seat will glow nevertheless,” says Kozin.
To someone observing from the train platform, things will look differently. Imagine a transparent train moving slowly alongside a station. A person standing inside the train and bouncing a ball off the floor will perceive it as moving straight up and straight down. But the outside observer will see a much more complex trajectory. Relative to this viewer, the ball is also moving forward due to the movement of the train. In physics, that’s referred to as Galilean transformation. Traditionally, scientists have believed that the difference in perspectives here is purely physical, as one of the observers is in motion while the other stands still.

But as the basic laws of electromagnetism were discovered, physicists’ understanding of the world was changed. In theory, these laws worked differently for moving and still objects, but actual experience shows that to not be the case. Scientists had long attempted to explain this phenomenon, but were not successful until Albert Einstein came along.
“Einstein showed that the laws of mechanics and Galilean transformations are based on simple phenomena with very low speeds,” explains Valerii Kozin. “No matter how fast we bounce the ball off the floor, we’ll never accelerate it to the speed of light or even a thousandth part of it. We don’t feel the difference, but time moves just the slightest bit slower in moving systems. Clocks on a train work differently from the clocks at the station. Even with a high-speed train, we’re talking about mere nanoseconds; even if you were to spend your entire life on a train, you still wouldn’t gain even a minute of extra time. But if someone were to get on a spaceship and travel at nearly the speed of light, then a decade-long space voyage would correspond to a whole era back on Earth. The interwovenness of space and time is necessary in order to make it so that the laws of physics are the same regardless of our reference system.”

And thus time and space have turned out to be interconnected. Since Einstein’s time, physicists regard them as space-time. Now, they regarded them as equals, meaning that if a phenomenon is observed in space, it must also be assumed that it can be observed in time.
Wilczek’s hypothesis
These basic principles of Einstein’s theory of relativity lay in the foundation of Frank Wilczek’s suggestion that time crystals must exist just like space crystals do. If there are structures that exhibit periodicity in space, then it is only logical to assume that there are ones that do the same with time.
Let’s say a system of atoms, caught in a special trap, is at complete rest at a temperature of absolute zero (−273.15 °C). It is not magnetized, but may change its internal magnetic properties with a certain periodicity of, say, one second while being at equilibrium. If such a structure were possible, it would violate the time-translational symmetry. During observation, we’d obtain the same results if the tests were done every second; if they were done at a higher or lesser frequency, the results would be different.
“Wilczek’s proposal was not strictly defined – it was more of a suggestion,” says Valerii Kozin. “Two Japanese scientists have formalized and analyzed that idea, coming to the conclusion that such objects cannot exist in realistic systems where the interactions between atoms occur at relatively short distances. Two atoms placed next to each other will interact, but two atoms spaced far apart won’t even “sense” one another.”

In 2014, a research team put forth a compromise: discrete time crystals, which only break the symmetry within a time scale set by a scientist. How does that work? A system of atoms is frozen to a near-absolute zero temperature. Then, the magnetic field affecting it is modified every nanosecond. The field is intermittently pointed upwards or downwards. In theory, the magnetization of the atoms would have to change at the same frequency – once a nanosecond.
“The scientists, however, were able to “break” that principle; the system’s magnetization vector changed not once a nanosecond, but once every two nanoseconds,” explains Valerii Kozin. “The researchers were impressed, their article was published in Nature, and experiments were carried out. But it still didn’t help solve the big question: if genuine time crystals, which change their magnetization not under the influence of outside forces, but completely on their own, could exist.”
Genuine time crystals
Researchers from ITMO University decided to find out if it is truly impossible to describe, even theoretically, a genuine time crystals. Could there be, despite the Japanese scientists’ scepticism, a system in which a hypothetical crystal would break the time-translational symmetry with no external catalyst? And it turns out there could.
“We’ve proposed a system that breaks the time-translational symmetry by way of non-local interactions,” says Kozin. “We examined a system in which one segment can directly influence other segments located far away. It was in this manner that we bypassed the theorem that said time crystals to be impossible, as it was limited only by short-range interactions within a system.”

To put it simply, imagine a long metal ruler. If you were to grab it in the middle and strike the right end, the left end will also begin to vibrate. This happens because the impact of the strike is transferred from the rightmost atom to the leftmost in a chain. That’s the principle of short-range interactions. But if we were to suppose that atoms could not only influence adjacent atoms by transferring pulses, energy, or something else, but instead influence all atoms within a chain – including those located at a distance – we get the principle of long-range interaction. This is not possible in our “regular” world, but scientists have already described systems within which such a thing would be possible.
“Even though it seems very unrealistic, we already know how to do something similar experimentally,” explains the researcher. “For instance, if you were to set a line of atoms in a trap and influence it in different ways, such as with electromagnetic pulses, you can effectively make the system experience these sorts of interactions in which the leftmost atom instantly “touches” the rightmost atom or several atoms at once.”
Theoretically, a material existing under such conditions may possess a crystal lattice and intermittently modify its properties, such as magnetization, spontaneously violating the time-translational symmetry. And that’s how the Nobel laureate’s theory, previously said to be impossible, was proven viable.
“This is a fundamental matter,” concludes Valerii Kozin. “What could be more fundamental than time and space? It has no real applied benefit. Although, perhaps, someday it will. Pretty much everything that physics has given to modern technology once began as fundamental research.”





