In the last 15 years, scientists all over the world have been actively researching various properties of graphene, a two-dimensional material that’s composed of carbon atoms arranged in a hexagonal lattice. Simply put, carbon atoms in graphene compose hexagonal cells. Such a structure of a crystal lattice makes it so that electrons in this material can behave as particles with a zero effective mass despite having mass. This is what gives graphene its unique properties.
What happens to electrons in graphene is described by the laws of quantum mechanics. This area of physics does not perceive the electron as a particle that moves around the atom’s nucleus, much like a planet moves around the sun, but as a wave of matter. Therefore, we can logically assume that there are similar materials in which other waves propagate in an unusual way. This is how scientists came up with the idea of photon graphene, a material with a lattice composed of hexagons but which is intended for working with photons rather than electrons.
After such materials were created, it turned out that what happens with light in them can be described with the equations from classical physics. At the same time, these phenomena are similar to quantum effects that emerge in regular graphene. For example, the Spin Hall effect when electrons with different spin divert in different directions when moving. Spin (something like a particle’s inner momentum) is a quantum category, there’s no description for it in classical physics.
Analogy principle
Then again, we all know that physics speaks the language of maths. If we represent a physical phenomena as equations, they can look really similar, despite the difference in their nature. This is how the analogy principle works in physics.
“I’ll give you a simple example from school physics," explains the article’s co-author Alexey Yulin, a leading researcher at ITMO’s Faculty of Physics and Engineering. "Let’s take a regular pendulum and swing it a bit. Then take an electric capacitor and connect it to an inductor. From the physical standpoint, the mechanical movement of the pendulum and the electrical processes in our second system are completely different. But if we write the equations that describe them in the simplest form, we’ll see that they are identical. As a result, we can apply everything that we know about the mechanical movement of a pendulum to an electrical oscillating circuit. If we have an interesting effect that can have a practical application, we can reproduce it in another system using this similarity.”
An international team of scientists that includes representatives of Sheffield University, the University of Iceland, and ITMO University showed that in photonic systems, when their classical description is valid, it’s possible to observe effects that are similar to quantum ones and are well-known in solid-state physics. While studying the properties of photonic graphene, scientists succeeded in identifying and describing an effect analogous to the Dresselhaus effect.
“We know that putting a material in a magnetic field can magnetize it," continues Alexey Yulin. "This happens because the energy of a particle with a nonzero spin depends on a magnetic field, and the applied magnetic field arranges the spins in one direction thus minimizing the system’s energy. But a particle’s energy can also depend on the correlation between its spin and orbital moment. And this is the so-called spin-orbit interaction. The Dresselhaus effect is when the energy of a particle that moves with a specific speed depends on its spin even at a zero magnetic field. In case of a photonic graphene, various polarizations of light play the spin’s role. We can create an equation that would describe the propagation of electrons in one case and the propagation of photons in the other. In both cases, the field is characterized by a four-component vector, and the movement equations are identical. This means that in both systems, we will observe the same effects.”
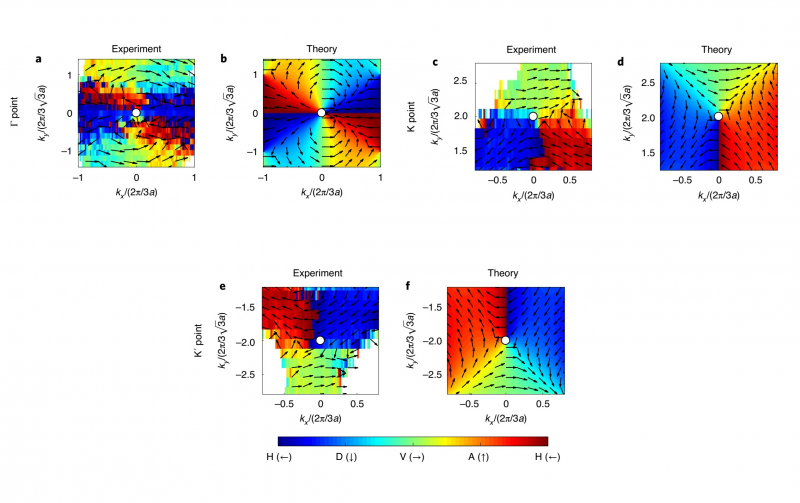
The research studied a photonic graphene that was excited by a focused laser emission falling under specific angles. For one, they studied in detail the instance when the correlation between the frequency of excitation and the wave vector was close to the Dirac cone. This takes place close to the so-called K points where quasi particles have zero mass.
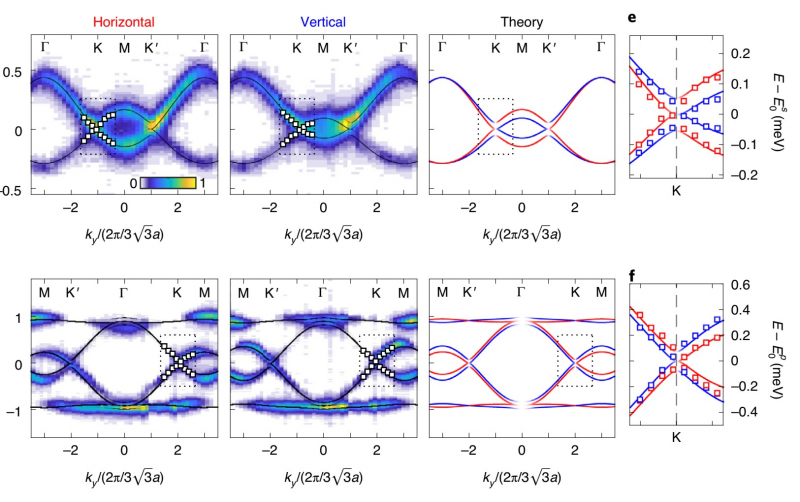
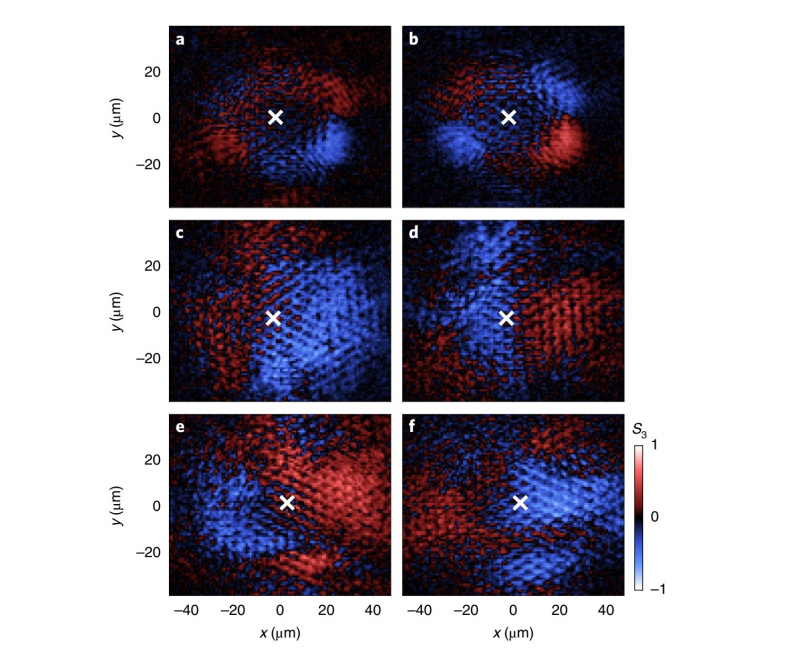
For comparison, the scientists also studied excitation of waves with small quasi impulses in the vicinity of the so-called Gamma points. In this case, quasi particles have a finite mass. It was shown that due to polarization effects, the electromagnetic wave frequency depends on its spatial period much like how electron energy depends on their impulse in the presence of spin-orbit interaction. It was experimentally demonstrated that the structure (we want to remind you that a wave’s structure is defined by four components) depends on the propagation direction differently if the system is excited in the vicinity of Gamma and K points.
The explanation of the observed effects was given in terms of the field theory, and it was also shown that the discovered effect can be interpreted as a movement in a non-Abelian gauge field. This way, the synthesis of solid-state physics and field theory methods showed its efficiency in researching purely optical effects in microstructured systems. The computing simulation made it possible to reproduce the experimental results with high precision and confirmed the analytical conclusions.
Prospects
The discovered effect can find various applications in optics, as it offers to make use of polarization as an instrument for controlling waves in two-dimensional wave structures.
One of the next directions that this research might take is studying the interaction of light in structures when the properties of a sample, among other things, depends on the intensity of the emission that propagates in it. Such systems are called nonlinear, and the propagation of high and low intensity waves in them can happen very differently. For one, in the context of photonic graphene, we can speak about a nonlinear (dependent on the intensity of light) spin-orbit interaction. This can be interesting not only from the fundamental standpoint but also useful in practical applications, for example for the generation of optical emission.
The fact that different physical systems can be identical at the abstract level of maths opens up new opportunities for theoretical physicists. The research methods that have been developed and successfully used for one kind of system can be adapted for the analysis of systems that have a different nature. With certain restrictions, we can expect that the use of theoretical physics methods will find application in researching biological and economic systems.
“It’s worth mentioning the importance of the fact that theoretical ideas and concepts can then be implemented experimentally, explains Alexey Yulin. And it can turn out that some properties that are hard to measure or control in one system have counterparts in another, ones that can be measured more easily. For example, controlling some properties of an electron in a solid is quite hard. But measuring the polarization properties of light in optics is a simpler task. For this reason, studying spin-orbital interactions in photonic graphene can lead to a deeper understanding of the effects that are similar to those in solid-state electronics. In other words, we are talking about creating simulators based on photonic graphene that would make it possible to model the dynamic of electronic excitation in a solid.”

Finally, the similarities discovered between the descriptions of processes in optics and solid-state physics encourages to look for the same similarities in other systems, for example acoustic graphene.
“In theory, similar effects can be observed in acoustics, explains Alexey Yulin. Acoustic waves in a solid can also be polarized, so we can expect similar effects for acoustic waves that propagate in an acoustic crystal with a hexagonal lattice. This is the fundamental value of our research: we show that at the level of maths, there’s no essential difference between a material, light, terahertz, and acoustic waves.”
Reference: C. E. Whittaker, T. Dowling, A. V. Nalitov, A. V. Yulin, B. Royall, E. Clarke, M. S. Skolnick, I. A. Shelykh & D. N. Krizhanovskii. Optical analogue of Dresselhaus spin–orbit interaction in photonic graphene. Nature Photonics, 2020/10.1038/s41566-020-00729-z